無料ダウンロード 平行四辺形 対角線 公式 285700

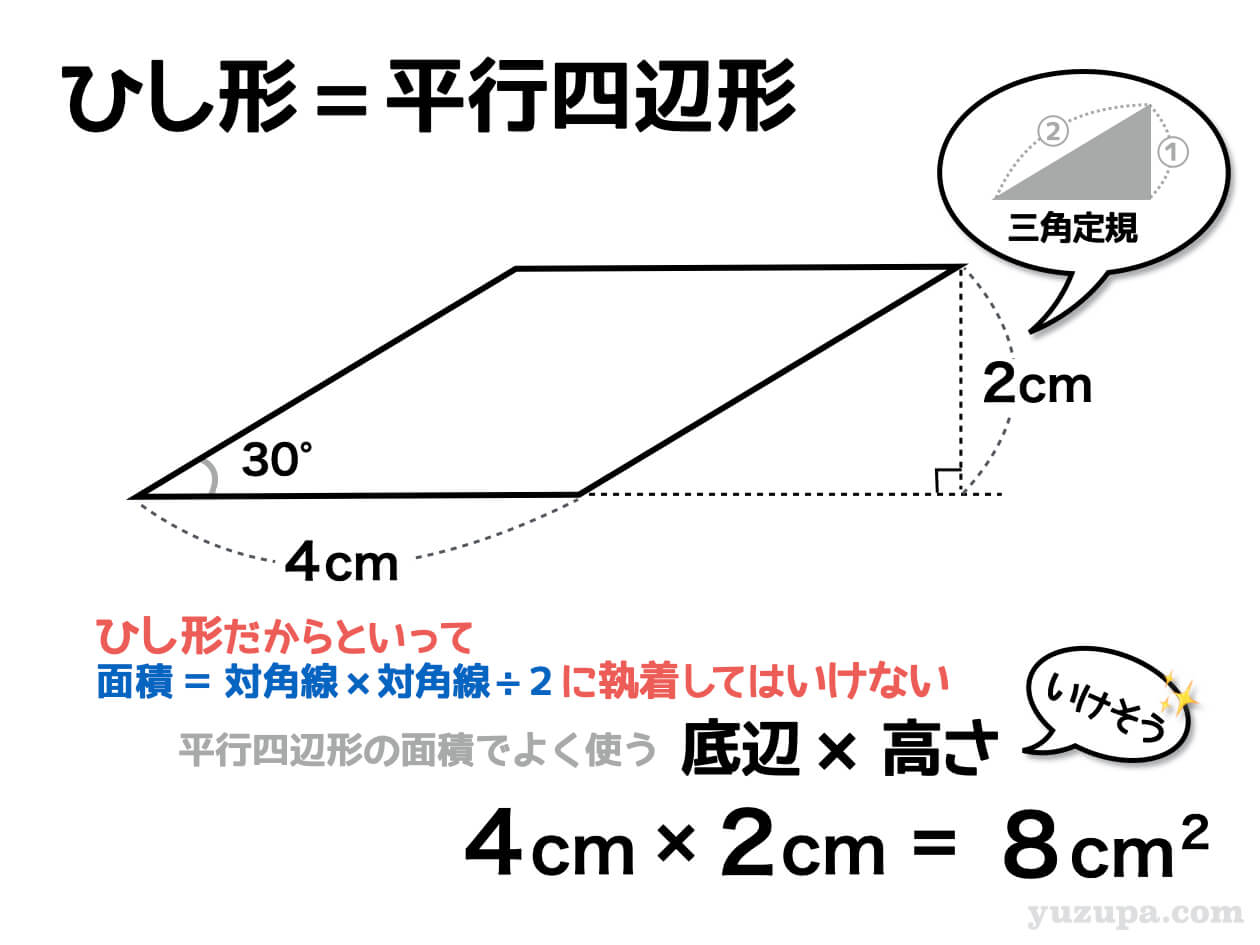
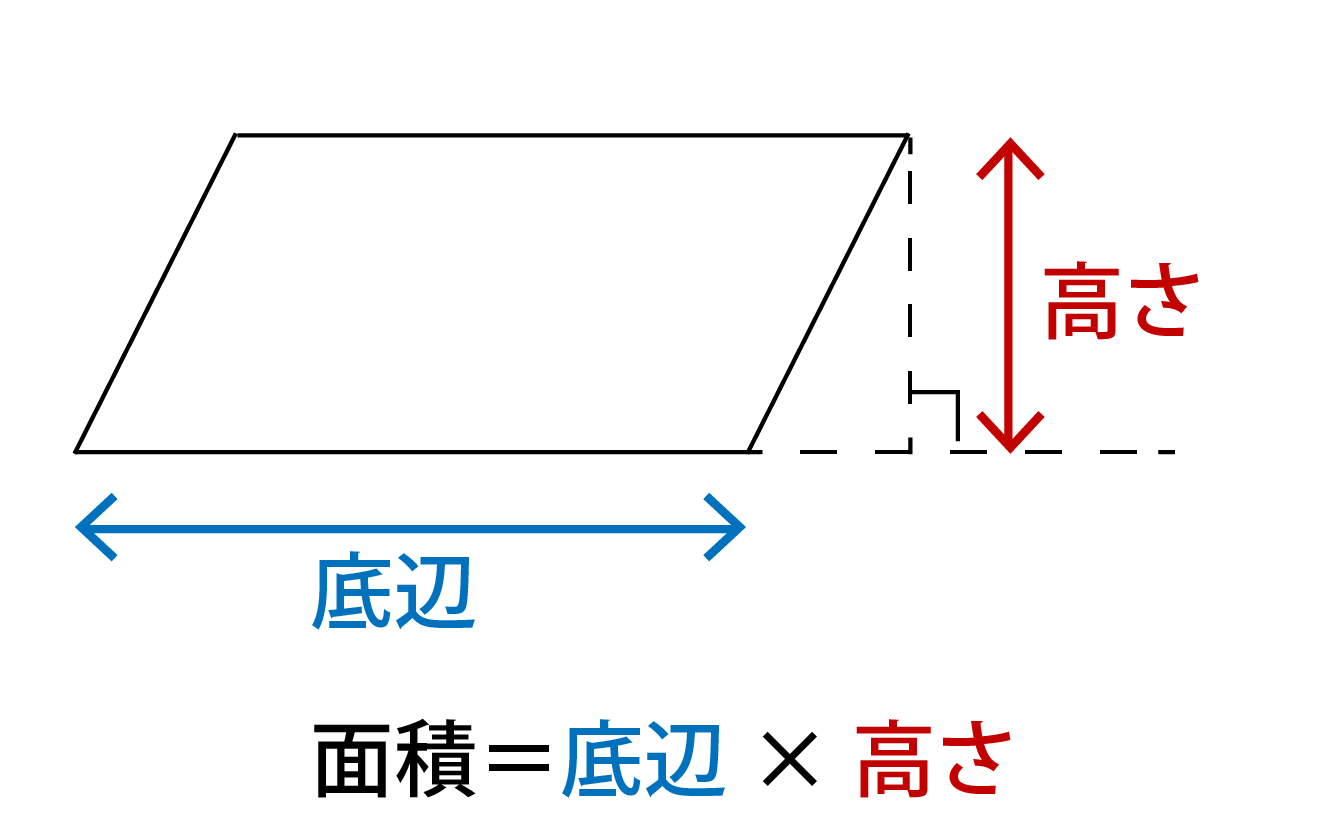
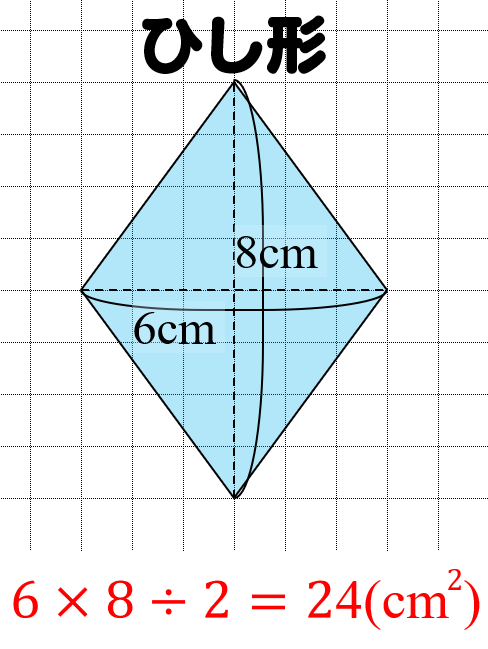
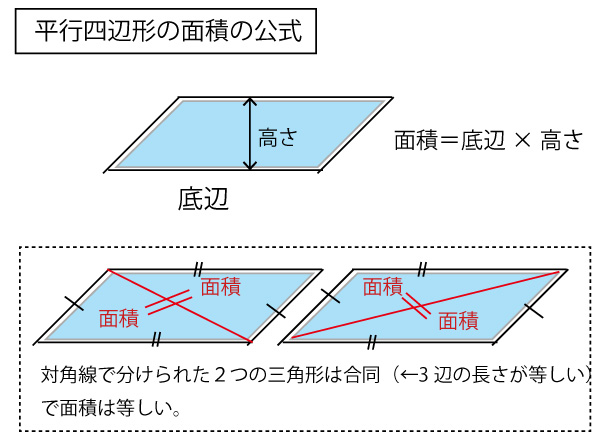
平行四辺形の面積は「底辺×高さ」で求められたよね？？ 菱形は平行四辺形ともいえるから、 この面積の公式も使えちゃうってわけさ。 じゃんじゃん計算していこう！！ まとめ：ひし形の面積の求め方は2通りおさえよう！ ひし形の面積の求め方は、 対角四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。ひし形の面積の公式 ひし形の面積は 2 2 つの対角線の長さをかけて2で割ったもの、つまり 『対角線×対角線÷2 ÷

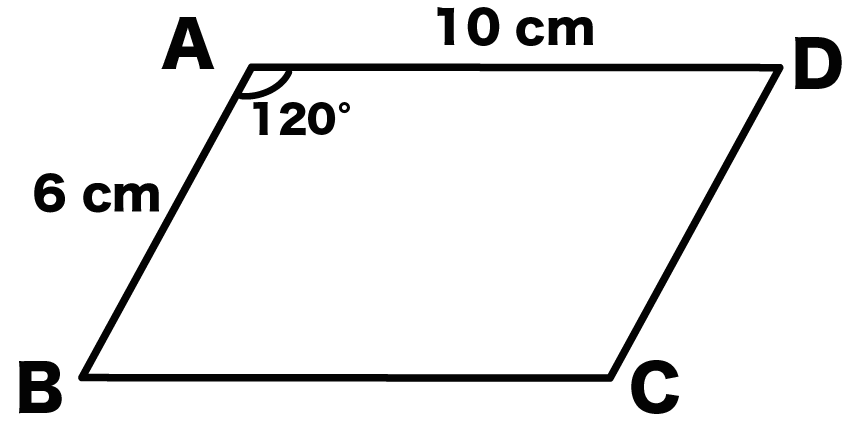
平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形 対角線 公式

平行四辺形 対角線 公式-対角線×もう一方の対角線÷2 で求められます。 ひし形は 横の対角線を横の辺、縦の対角線の半分を縦の辺とした長方形に変えられる からです。ひし形を対角線で4つに切ってみると分かります。 ひし形は平行四辺形の1つです。辺の長さと高さが分かってカイト 今回は、平行四辺形になるな。 ミズキ 平行四辺形なら、もう面積の求め方は分かるね。 カイト わかんねぇーって奴は、前の動画で俺が必死こいて解いてるから、見てくれよな。 ミズキ 平行四辺形の公式は「底辺×高さ」だね。 ミズキ この平行

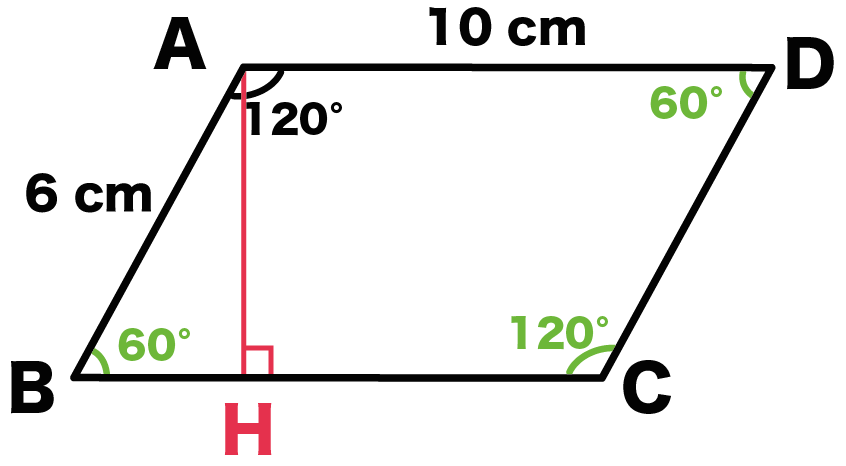
平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する数学・算数 平行四辺形の証明 平行四辺形の証明において、 （1）対辺は等しい。 （2）対角は等しい。 （3）対角線は互いに他を二等分する。 という三つの証明を各々どう証明すればよいのかと聞かれて 質問No平行四辺形はたくさんの性質があります。 ①2組の対辺はそれぞれ等しい ②2組の対角はそれぞれ等しい ③対角線はそれぞれの中点で交わる 定理：1組の対辺が平行で、その長さが等しい たくさんありはしますが、平行四辺形とイメージするとでてくる

平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\)・ 平行四辺形の求積公式を考え，それを適用 する。 平行四辺形の面積＝底辺×高さ ・ 高さが平行四辺形の外にある問題場面で， 底辺と高さに着目して求積公式を適用する。 平行四辺形3 abcdの対角線bd上に頂点aとcから垂線を下ろしその交点をe,fとする。平行線と比の利用、辺の長さを求める問題をパターン別解説！←今回の記事 木の高さを求める方法について解説！ 中点連結定理を使った問題を解説！ 相似の面積比を求める問題をイチからやってみよう！ 面積比！平行四辺形の面積問題を解説！ 面積比！

これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて \(3cm\) 横 \(4cm\) の長方形」になるので \(たて×横=3×4=12cm^2\) からも求められますね。 ③ ひし形の面積 ひし形の面積は、\(「面積=たての対角線×横の対角線÷2」\) で求められます。平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 12 』 で求めることができます。 平行四辺形の一種でもあるので、底辺と高さが分かっていれば『底辺×高さ』でも求められます。 たとえば

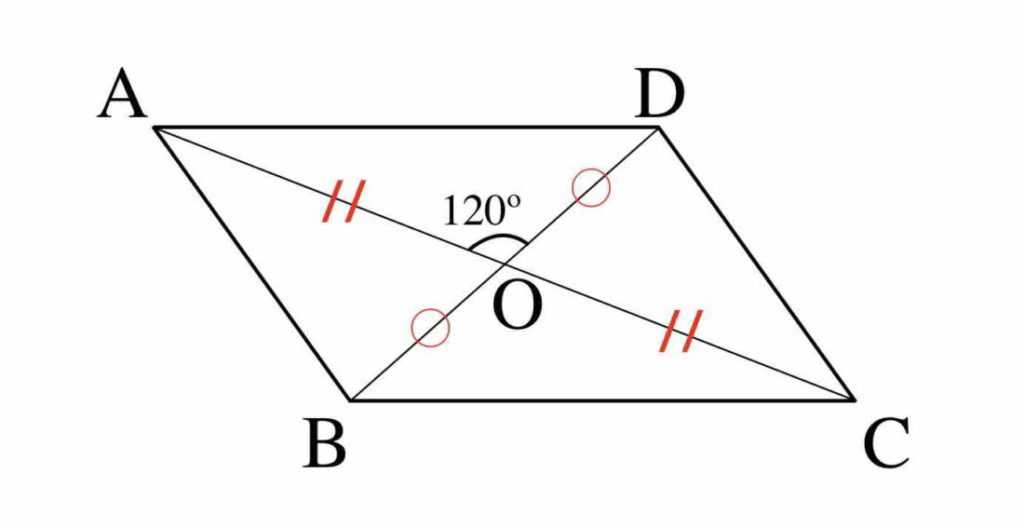
三角比を用いた面積計算をマスターしよう スタディクラブ情報局

平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室

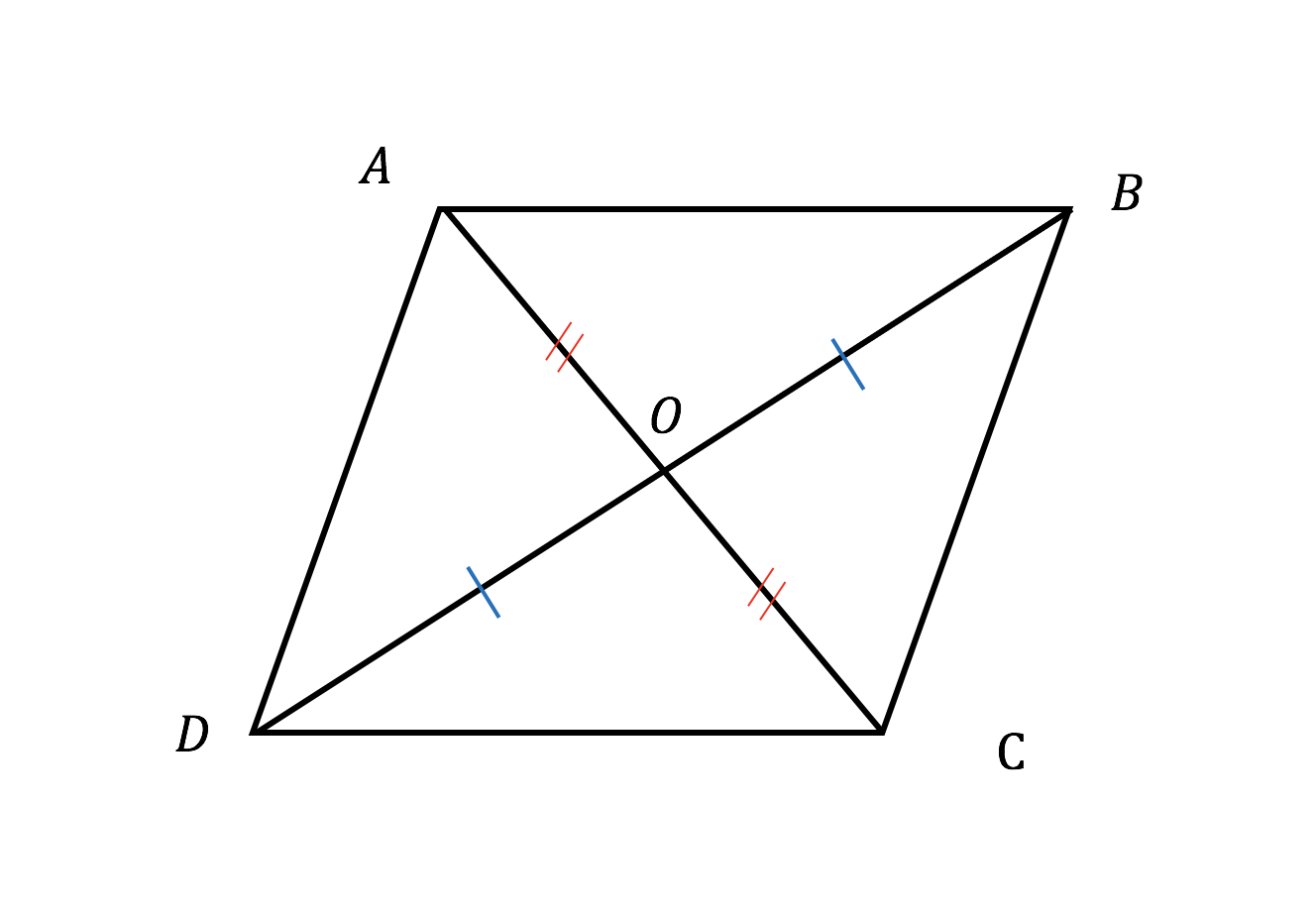
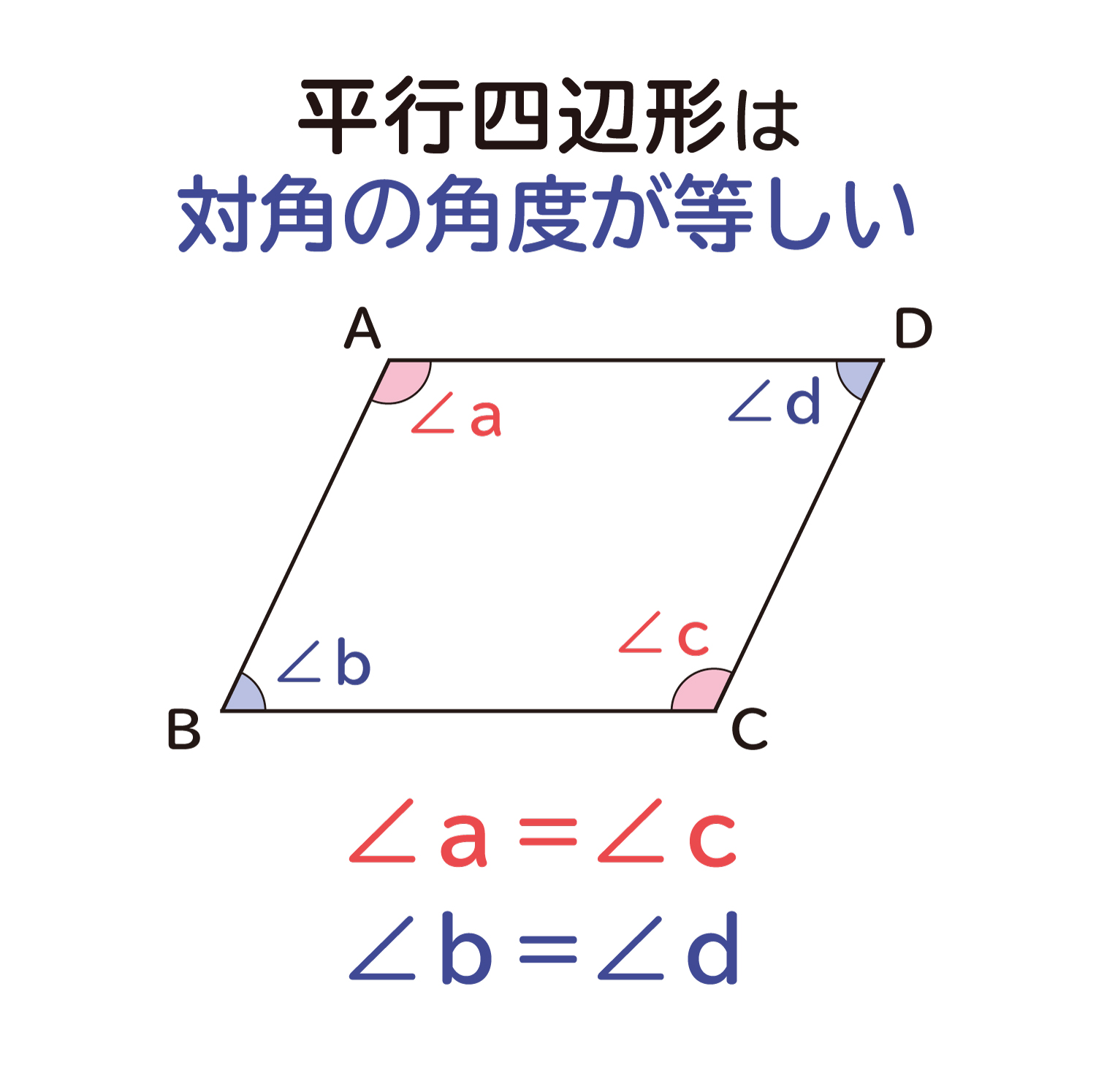
De//bcより平行線の同位角は等しいので∠aed=∠ecf ab//efより平行線の同位角は等しいので∠ead=∠cef よって2組の角がそれぞれ等しいので ade∽ efc 相似な三角形の対応する辺の比は等しいので adef=aeec 四角形dbfeは平行四辺形なので ef=db《対角線の長さの求め方》 ひし形の面積を求める公式＝対角線×対角線÷2より 対角線×対角線÷2＝54（㎠） ここで片方の対角線の長さが6cmとわかっているので、もう片方の対角線の長さを （㎝）とすると これを計算して ×3＝54 答え 18cm・平行四辺形には、下のような3つの性質があります。 1．対辺の長さが等しい 2．対角の角度が等しい 3．対角線は中点で交わる 今回、1つ目の平行四辺形の性質である、 対辺の長さが等しい ことを確認していきたいと思います。

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

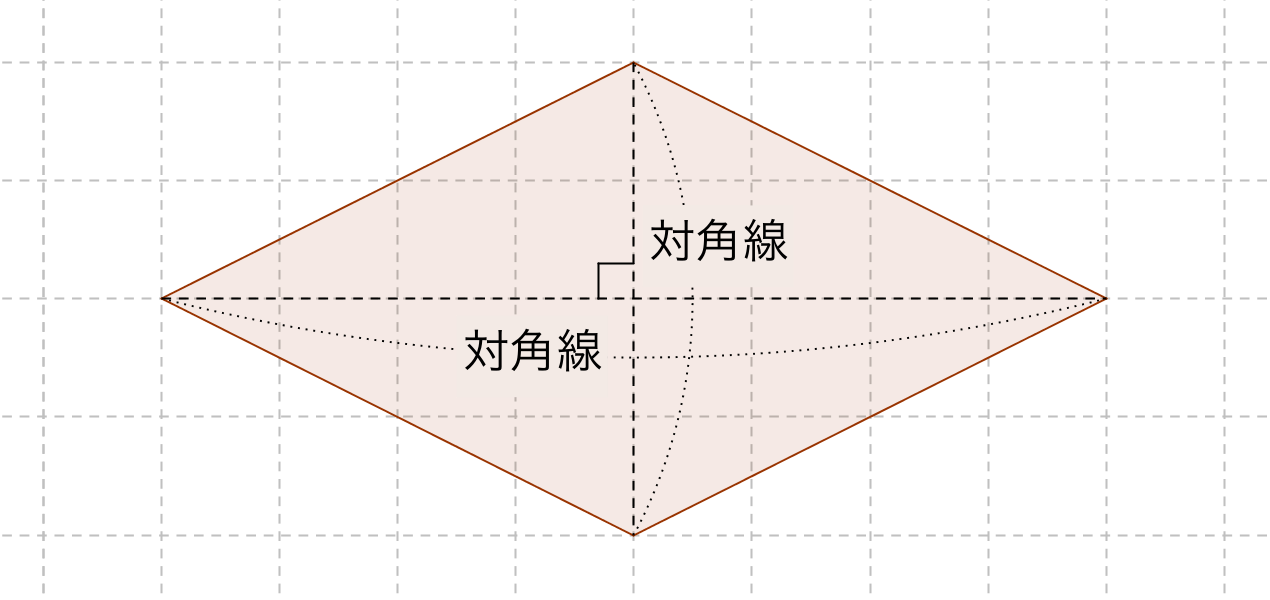
ひし形の面積の公式 算数の公式

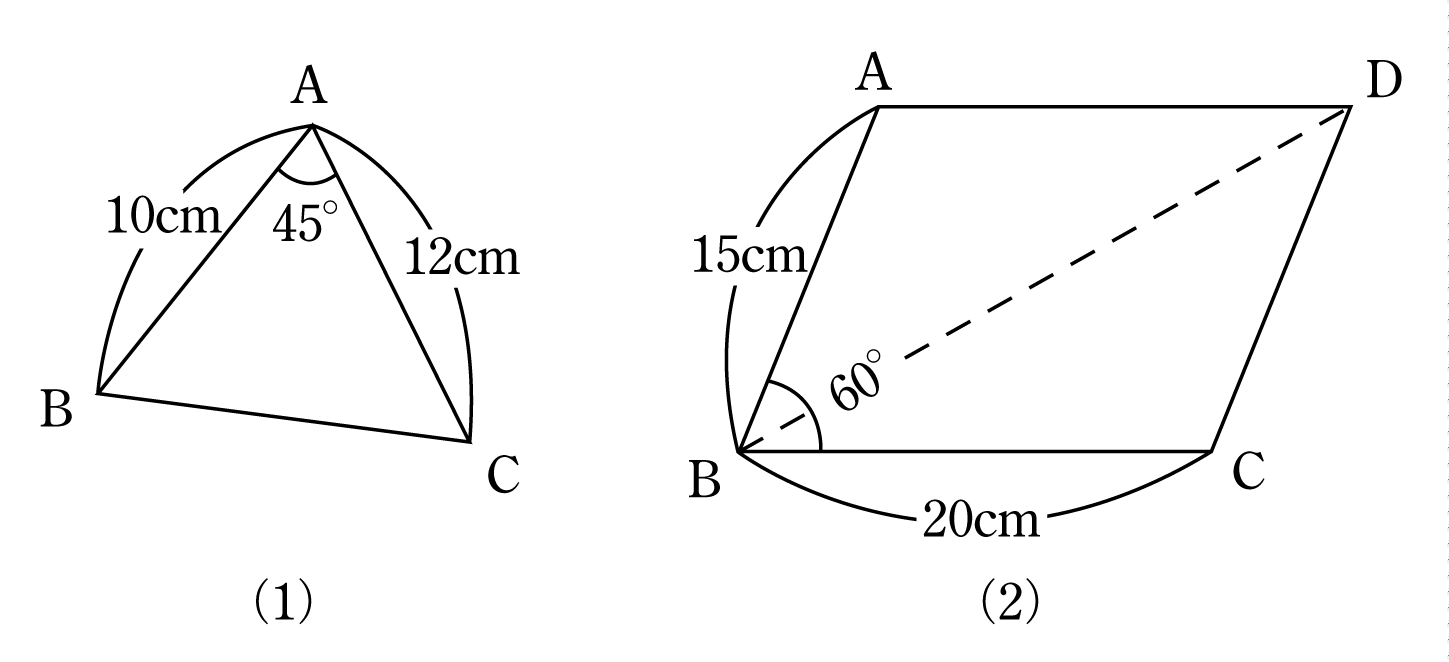
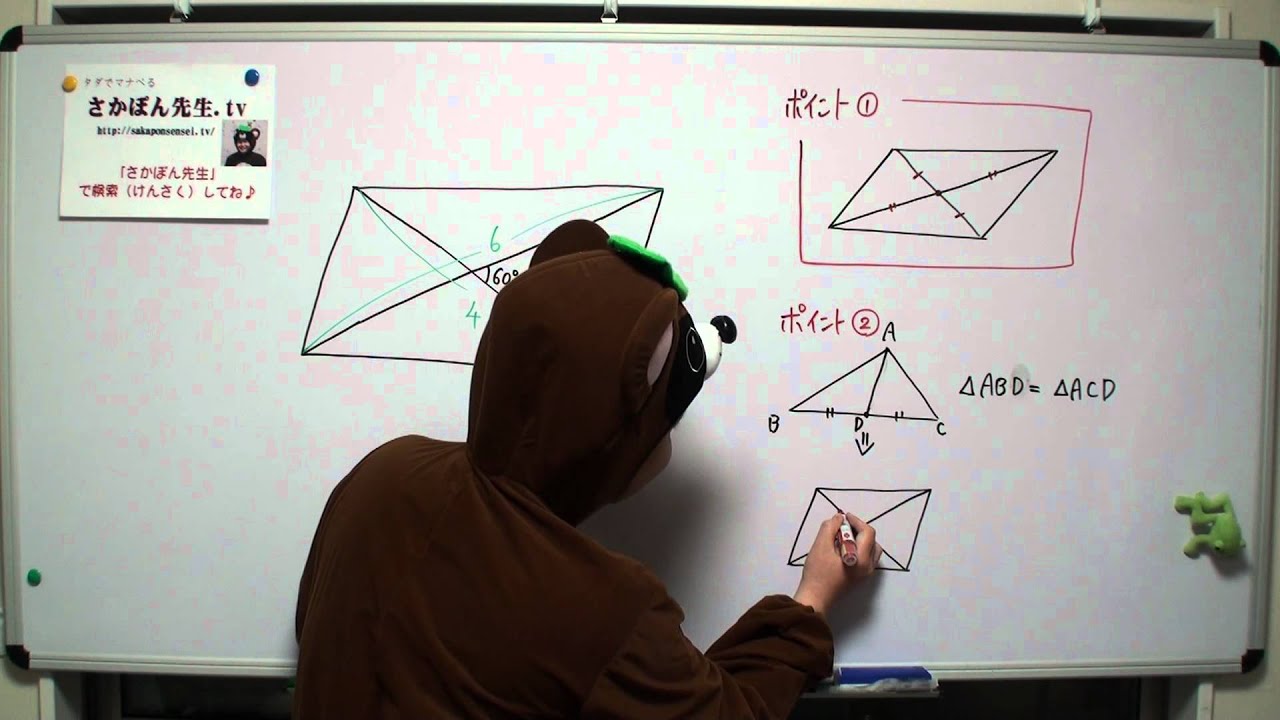
平行四辺形の面積を対角線の長さと角度から求める $2$ つの対角線の長さが $4$ , $6$ 、その2辺のなす角が $60°$ のとき、その平行四辺形の面積を求めよ 対角線は他の対角線の中点で交わるってことを利用して、図にするとこうなるね逆に、どの平行四辺形も対応する斜めの線2本と横の線2本があります。この対応に重複や漏れはないので、平行四辺形の個数を数えることは、「 斜めの線と横の線の選び方 」を数えることと同じになることがわかります。 斜めの線は5本あってそこから231 平行四辺形の性質その1：対辺の長さが等しい 32 平行四辺形の性質その2：対角の大きさが等しい 33 平行四辺形の性質その3：対角線が他の対角線の中点を通る 4 平行四辺形の面積 (公式・証明) 5 平行四辺形の成立条件 51 平行四辺形の成立条件その1：2

ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

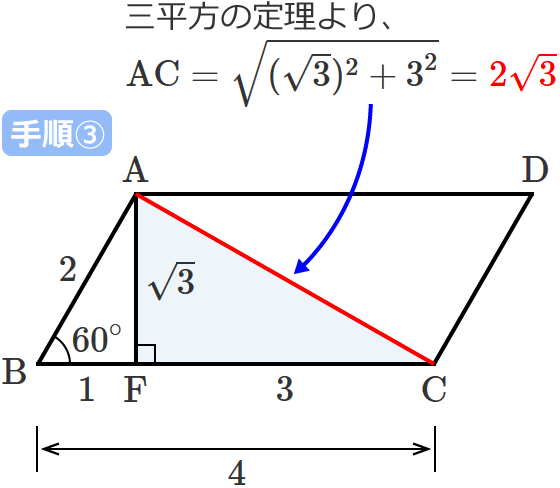
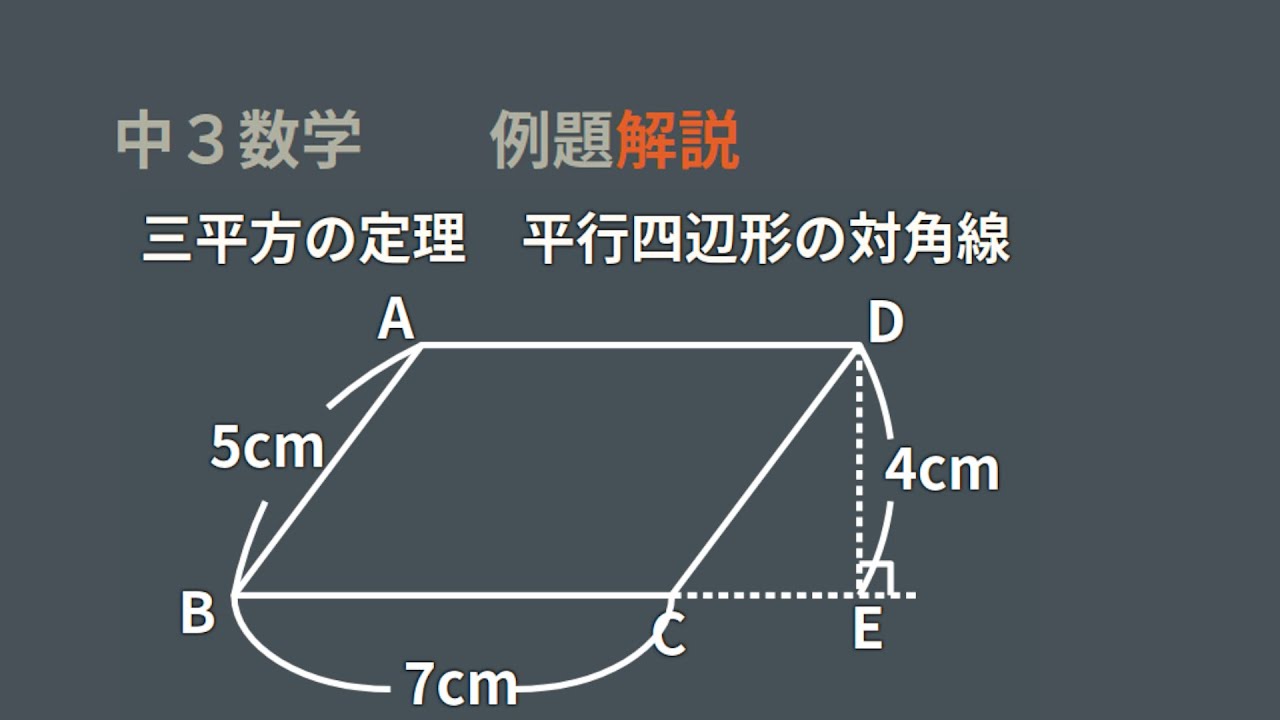
ミズキ こんにちは、ミズキです。 ミズキ 今回は様々な四角形について、一緒に考えていきましょう。 カイト よろしくな！ ミズキ！ ミズキ アオイくんにも、手伝ってもらいます。 アオイ カイにも分かるように、頑張って教えよう。 ミズキ さて、それでは、まず平行四辺形の面積の公式にF 4cm 3cm 対角線ac ≫ aからbcに垂線を引き交点をfとする。 ≫ 直角三角形abfで三平方の定理を使うと 5 2 =4 2 bf 2 bf 2 =2516 bf 2 =9 bf=±3 bf>0より bf=3 ≫ bc=7なのでfc=4過去ブログの転載です。 今も多分変わっていないと思うのですが、小学校で登場する図形のうち面積とか体積を公式として求められるものには次のようなのがありました。 ① 長方形の面積（縦×横）② 正方形の面積（一辺×一辺）③ 平行四辺形の面積（底辺×高さ）④ 三角形の面積（底

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clearnote

以下の2つのことを、複素数を用いて示せという問題なのですが、どのようにして示せばいいのかわかりません。 どなたか教えてください。 1)平行四辺形の対角線は互いに二等分することを示せ。 2)ひし形の対角線は互いに直交するこ平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦！ それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基平行四辺形の面積（底辺と高さから） 平行四辺形の面積（2辺と夾角から） 円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積（中心角

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

∠a＝∠cbe（平行線になる条件） AB//DC AD//BC ＜戻る＞ 4 対角線が、それぞれの中点で交わる。 ABOと CDOで AO＝CO 1 BO＝DO 2 対頂角）3 1，2，3より2辺とその間の角がそれぞれ等しいので平行四辺形の性質 ③2組の向かい合う角はそれぞれ等しい ④対角線は互いに他を2等分する 10 三角形の辺と平行線 11 中点連結定理 四角形は円に 内接する ①対角の和が180°

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

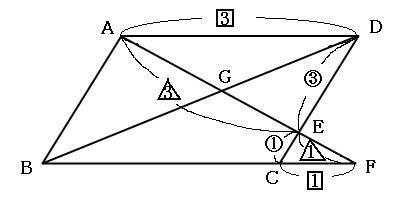
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

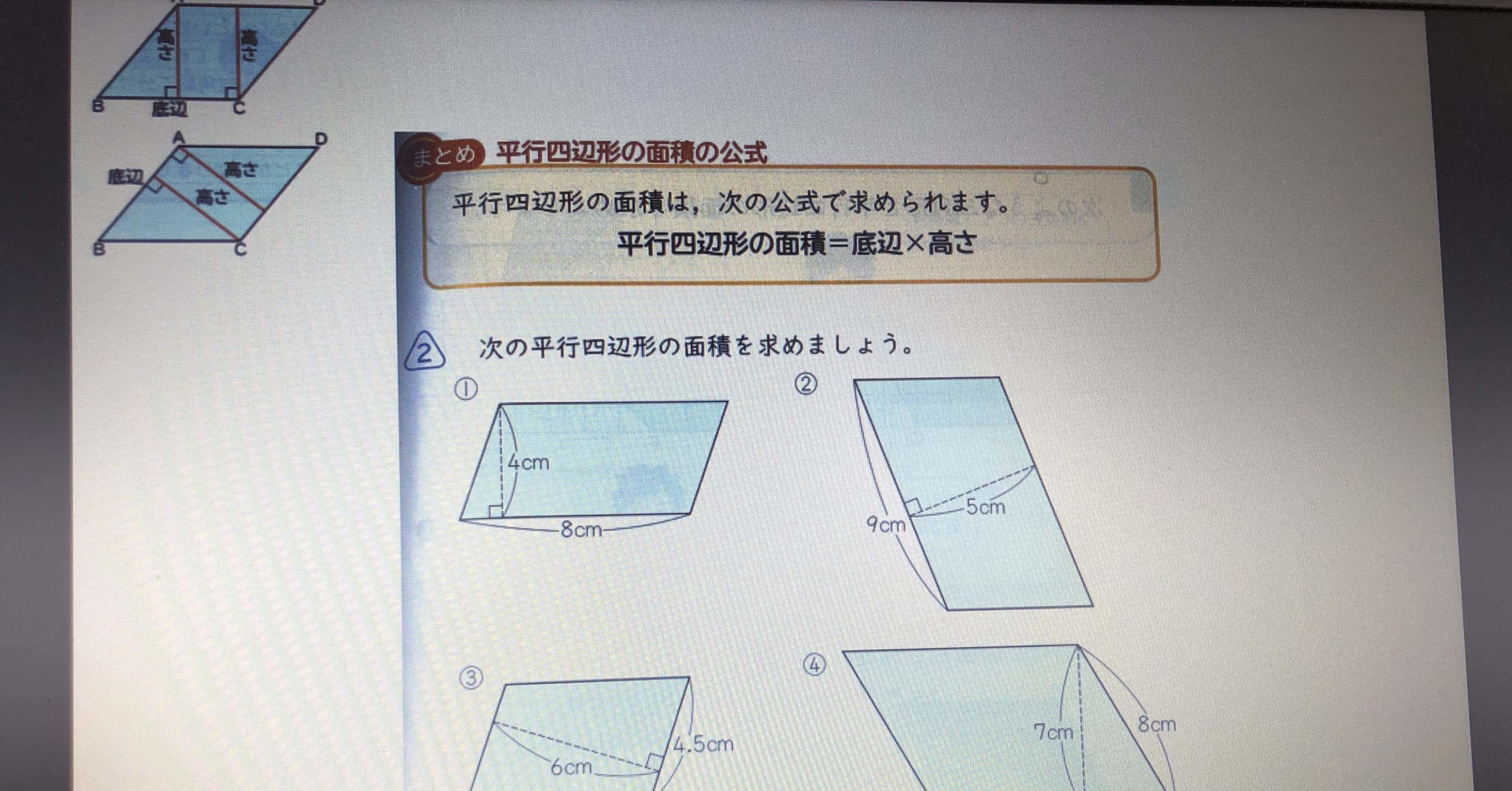
三角形を基に考えるのか 長方形を基に考えるのか 平行四辺形の面積を求める公式 清水智 Shimizu Satoshi 教育ictコンサルタント Google認定教育者レベル2 Note

Lh3 Googleusercontent Com Proxy O437ywmefmlf24yexvmqf12xteroedqcngt3cbo pe Xauw5xyb0y6zhlyr9ljdbm Oe7jseg Cvcz3ysaoqdwzu5zyc7gjwoh4kt0xshhihkl7oiw Cdqb51h0cla E Vrped03eqpfvg6zhls

小4算数 Aと同じ角度はどれ 垂直と平行といろいろな四角形 台形 平行四辺形 ひし形 の解き方 教え方 いっしょに勉強しよ

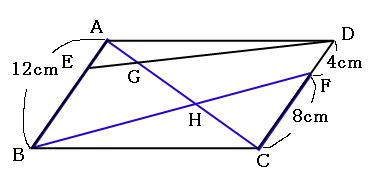
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

平行四辺形の角の二等分線

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo

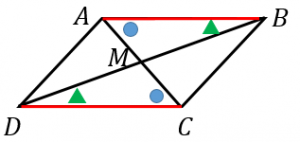
平行四辺形の3つの性質とその証明 具体例で学ぶ数学

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

数学の問題の解き方を教えてください Clearnote

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

今月の問題 平行四辺形

小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

平行四辺形の面積を対角線と角度から求める問題 Youtube

５年算数三角形と四角形の面積2 教え方 台形 ひし形

3

平行四辺形の座標 数学ii By Okボーイ マナペディア

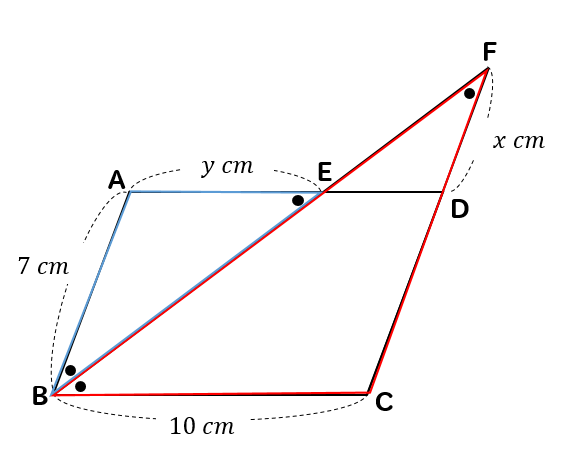
平行四辺形の対角線の長さの求め方

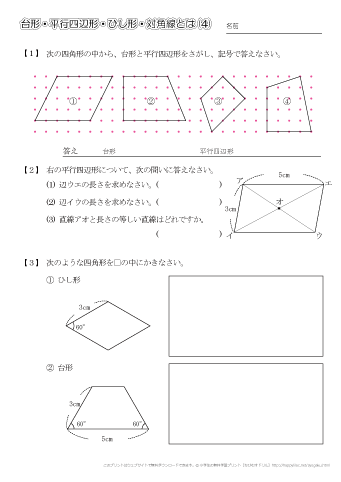
小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

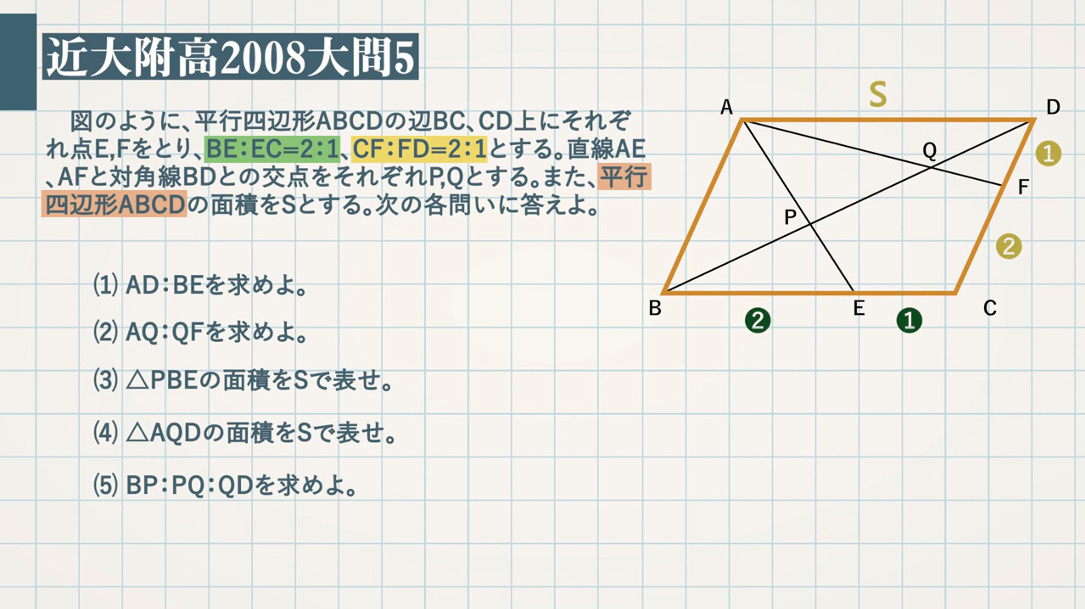
平行四辺形と比 教遊者

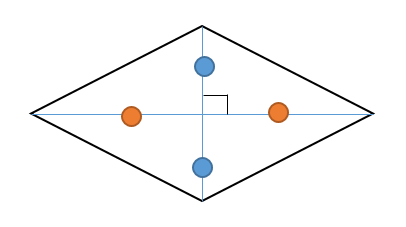
小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー

平行四辺形の対角線の長さの求め方

中学生ならおぼえたい 平行四辺形になる5つの条件 Qikeru 学びを楽しくわかりやすく

ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係

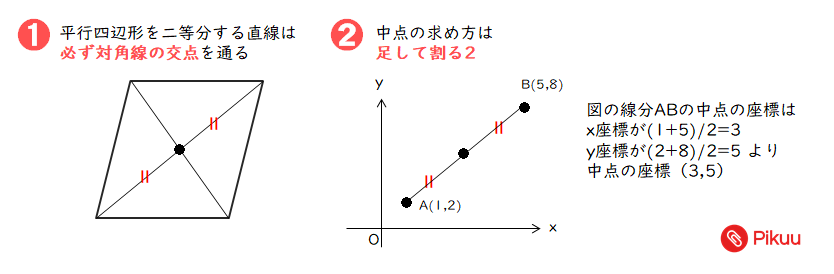
中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu

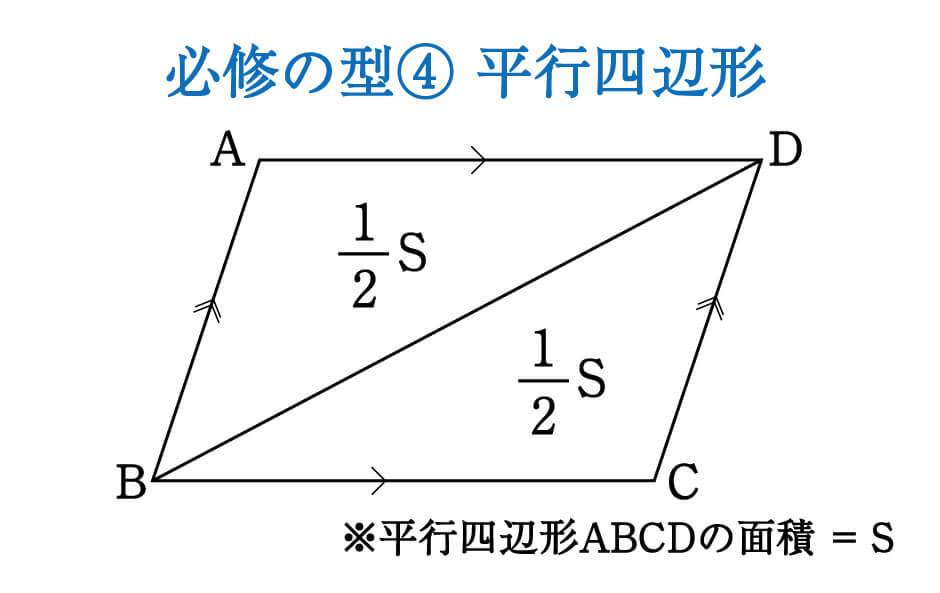
数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

力の平行四辺形

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

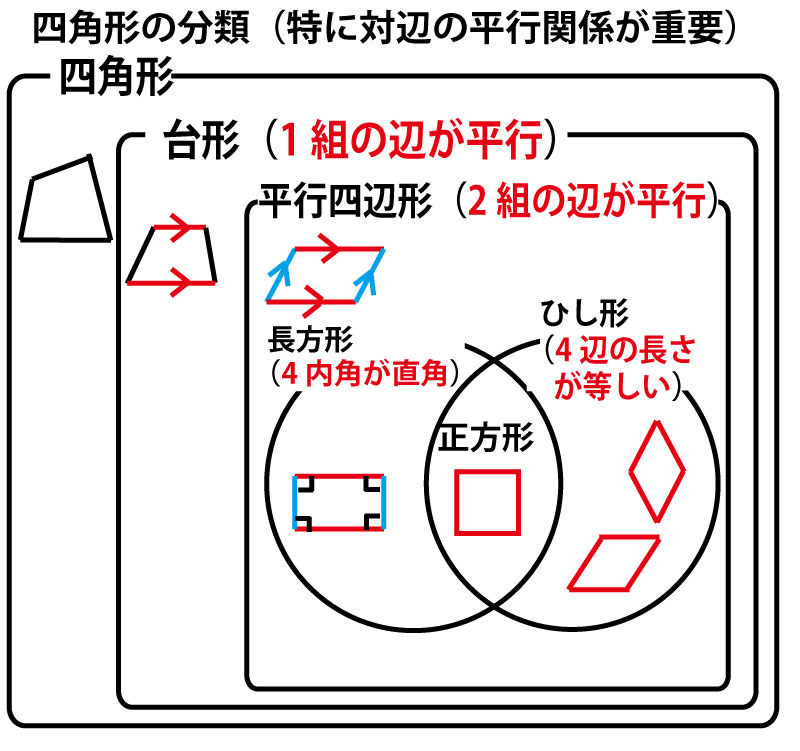
菱形定義 平行四辺形 ひし形 長方形 正方形の違い Vsrius

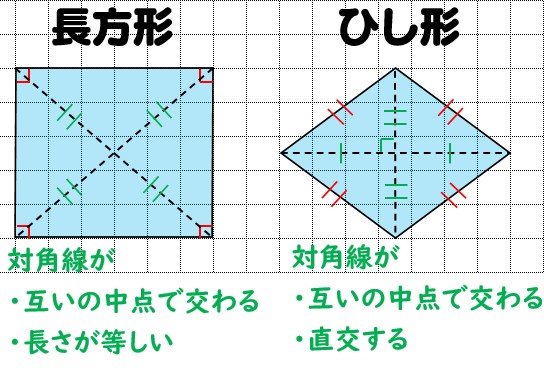
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

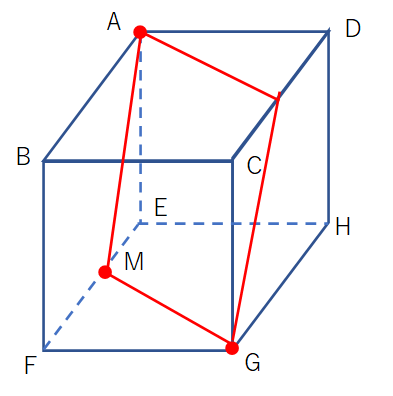
立体切断の切り口 これひし形なの 長方形かと思った の解き方について 算田数太郎の中学受験ブログ

平行四辺形の対角線の角度について この条件の時の角度a Bを文字で表 Yahoo 知恵袋

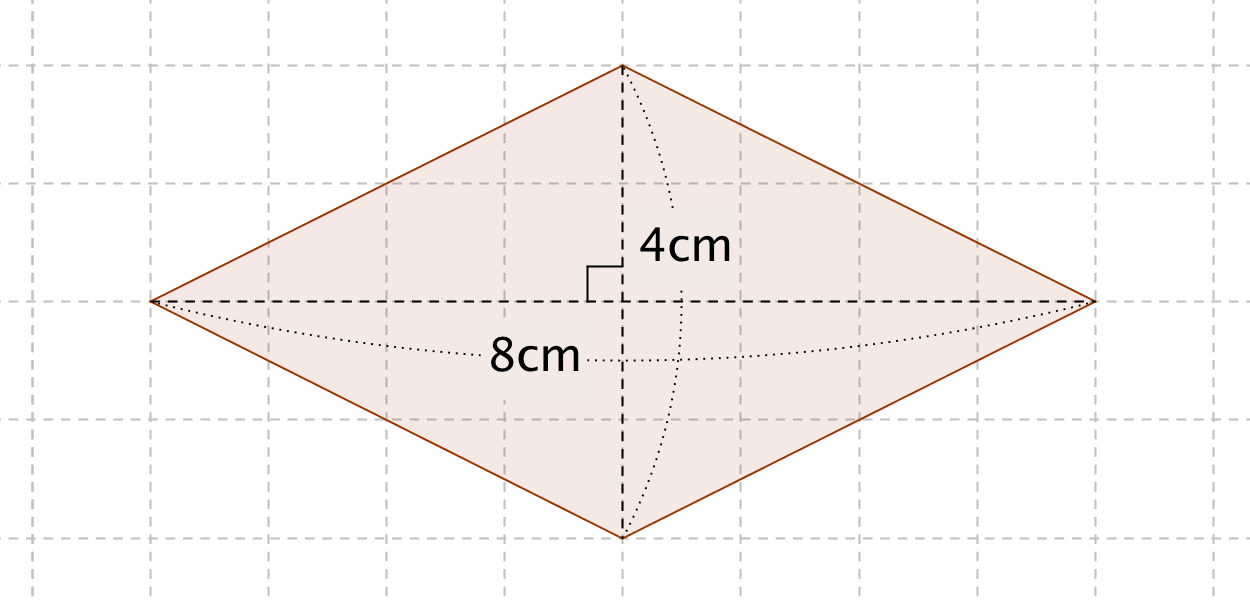
ひし形の面積の公式 算数の公式

平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生

ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題

小５ 算数 小５ ４４ ひし形の面積 Youtube

公式なんて覚えない ひし形の面積は直感的に考えよう

1

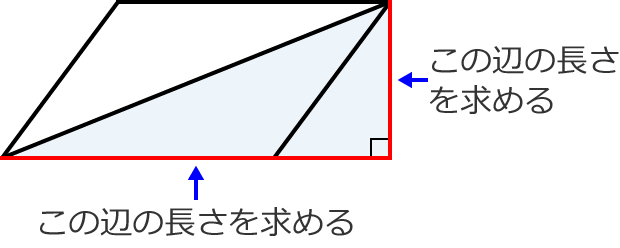
平行四辺形の対角線の長さの求め方

高校数学b ベクトルの成分表示と平行四辺形 受験の月

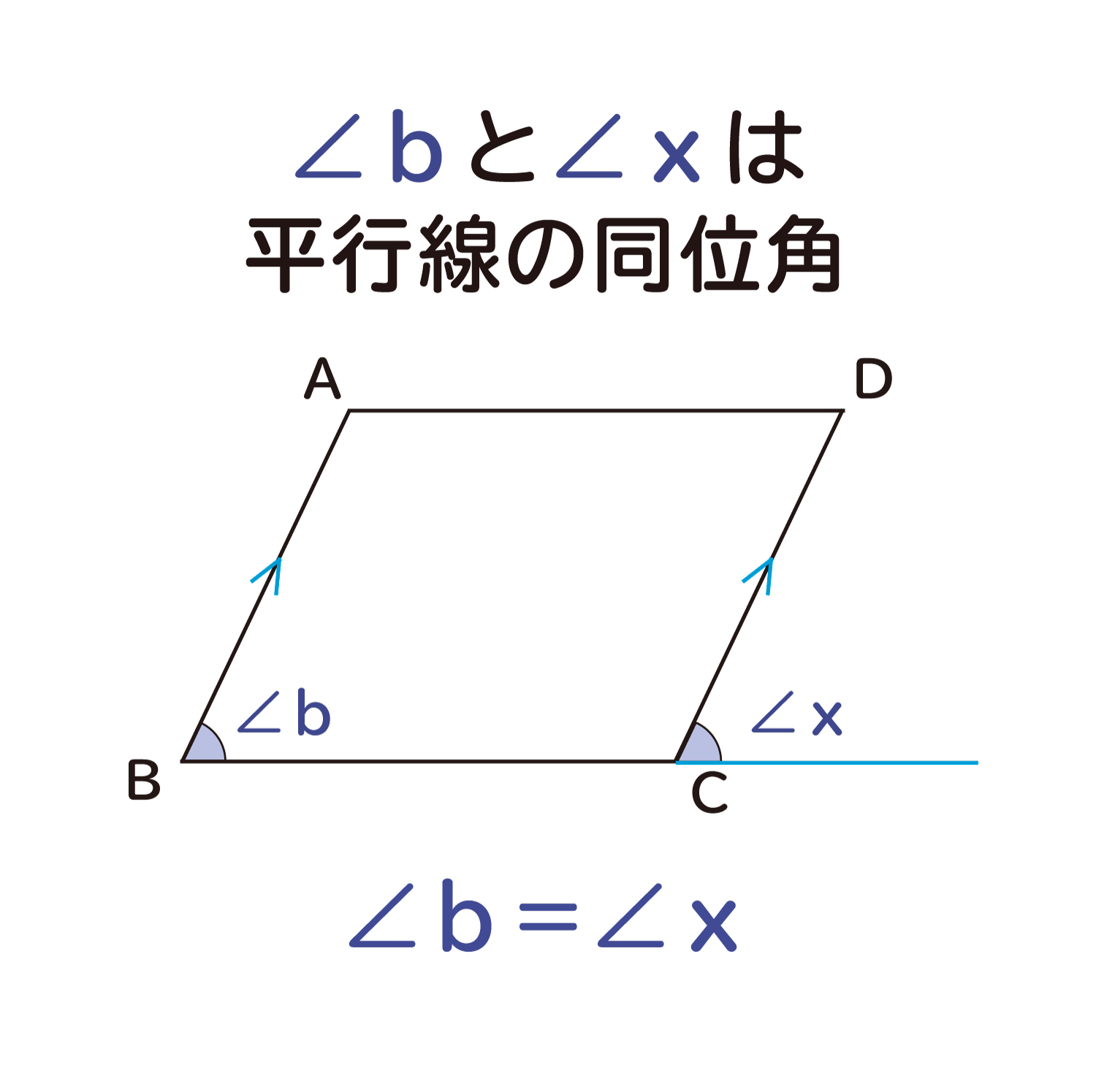
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校

3

平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室

ひし形 の 対角線 の 長 さ

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

四角形と三角形の面積

平行四辺形の面積の求め方 公式と計算例

平行四辺形の二つの対角線の長さが違う理由って何ですか Aklv721 Yahoo 知恵袋

公式なんて覚えない ひし形の面積は直感的に考えよう

平行四辺形の面積の求め方 公式と計算例

平行四辺形対角線の求め方と面積について 対角線ａｃの長さの Yahoo 知恵袋

勉強しよう数学 ひし形の対角線の直交の公式と２重平行四辺形の面積の公式

平行四辺形で知っておくべきこと 苦手な数学を簡単に

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行 四辺 形 対角線 平行四辺形とは 定義 条件 性質や面積の公式 証明問題

平行四辺形の法則とは 1分でわかる意味 計算 証明と角度の関係

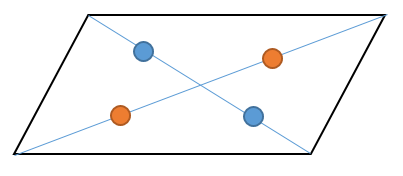
小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー

平行四辺形の対角線の長さの求め方

面積の求め方は ずらす わける ふやす 授業研究のブログ

相似 平行四辺形と面積比の問題を徹底解説 数スタ

中３数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ

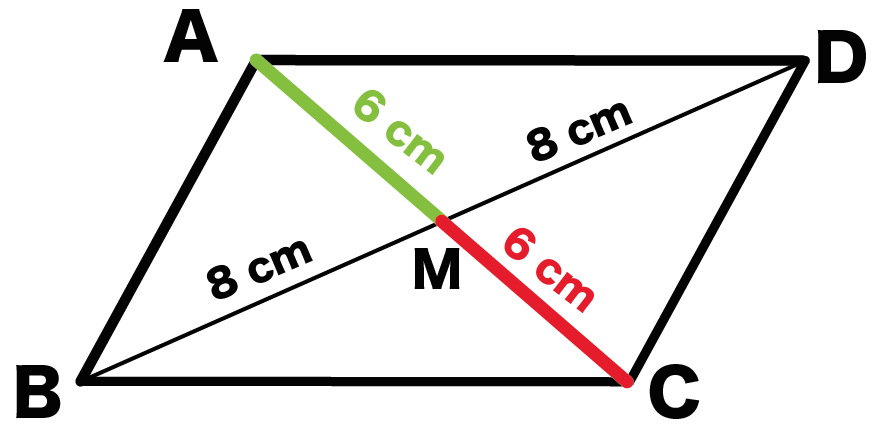
平行四辺形の対角線はそれぞれの中点で交わることの証明 をしないとい 中学校 教えて Goo

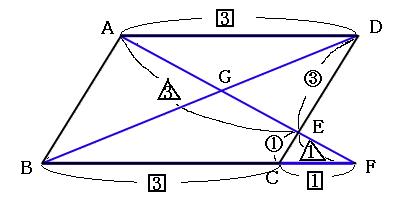
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

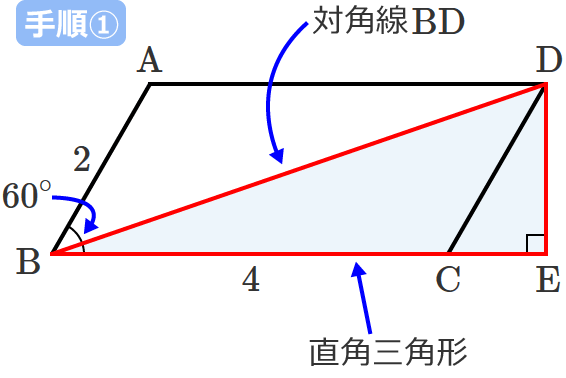
平行四辺形の対角線の長さの求め方

21年 千葉県公立高校入試 数学 第3問 二次関数 配点計15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

勉強しよう数学 余弦定理に類似した公式の多さの解決策はベクトル

三平方の定理 平行四辺形の対角線

平行四辺形の面積の求め方 公式と計算例

平行四辺形の対角線の長さの求め方

Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd

1

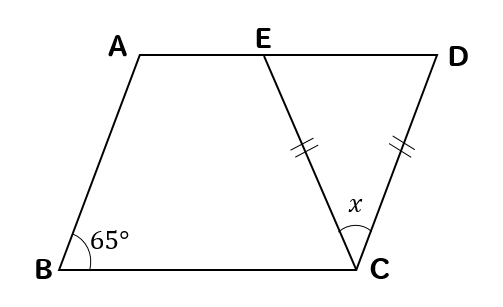
平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

平行四辺形 Wikipedia

平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形の辺や角を求める Youtube

コレクション 平行四辺形 対角線 長さ 等しい ニスヌーピー 壁紙